From DH to ECDH
motivation:
we want to remain the hardness of the regarding DLP while reduce the key size dramatically.
Then we need to find a public key family. the idea is to find another cyclic group beyond Z*p in which the DLP is difficult.
EC
The equation of curve in EC:
\[y^2 = x^3+ax+b\]
the elliptic curve over $Z^p$ is all points on the above equation together with a imaginary point at infinity, where $a,b\in Z^p$ and $4a^3+27b^2$ $\neq$ 0 mod p.
we want to have a cyclic group for DLP, we need:
- set of element
- group operation(closed,associative)
- a generator(the element which order equals to the group cardinality)
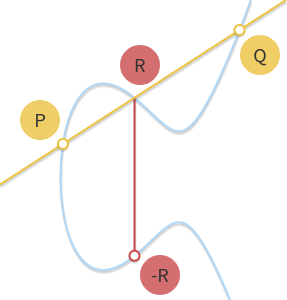
’+’ operator :
how to perform ‘P+Q’ geometrically:
adding:
> draw a straight line of PQ and it intersects the curve at another point, take the mirror of that point by X axis.
point doubling(P+P)
> draw the tangential line for P and get the intersect point then take the mirror of that point by the X axis.
A formal solution to compute:
$X_3 = S^2 - X_1 - X_2$ mod p (1);
$Y_3 = S(X_1-X_3)-Y_1$ mod p (2);
$S = {\begin{matrix} \frac{Y_2-Y_1}{X_2-X_1} mod\ p\ \ for \ point\ addition\\frac{3X^2+a}{2Y_1} mod \ p\ \ for \ point \ doubling \end{matrix}$
note: in DLP, ‘/’ operator mean inverse. $A/B = A*B^-1$
what is the identity element? P+I = P for all P. ( The imaginary point)
what is the reverse of one point : P = (X,Y) , -P = (X,-Y)
Example:




How may points lies on the curve E(#E, the cardinality of this group) is computationally hard.
Given an elliptic curve E modulo P, the number of points on the curve is denoted By #E. and $P+1-2\sqrt{P}$ <#E< $P+1+2\sqrt{P}$
ECDH
The Discrete Logarithm problem:
given E,P,T s.t dP=T, it is computatinally hard to compute d.
‘d is the number of hops on the curve’
ECDH: ‘d’ private key, $d\in$ {2,…..,#E}mod p
The process:
- 1 st phase: given E: $y^2=x^3+ax+b$, primititive element P(xp,yp) //the generator as public key
-
2nd phase:
Alice : chose a from {2,…..,#E-1} , A = a*P(P+P+….+P,a times)
Bob : chose b from {2,…..,#E-1} , B = b*P(P+P+….+P,b times)
and they exchange A and B.
Alice: (aB) = $(X_{AB},Y_{AB})$ , Bob : (bA) = $(X_{AB},Y_{AB})$
use $X_{AB}$ as the shared key.
personally, I think the hardness comes from the ‘+” operation in ECDH, EC only increase the cardinality by at most $\sqrt{P}$, however, In every ‘+’ operation, we need to do a inverse computation which almost increases the hardness by $\log{P}$.