Multi-task learning
https://ruder.io/multi-task/ ## hard parameter sharing It is generally applied by sharing the hidden layer between all tasks, while keeping several task-specific output layers.
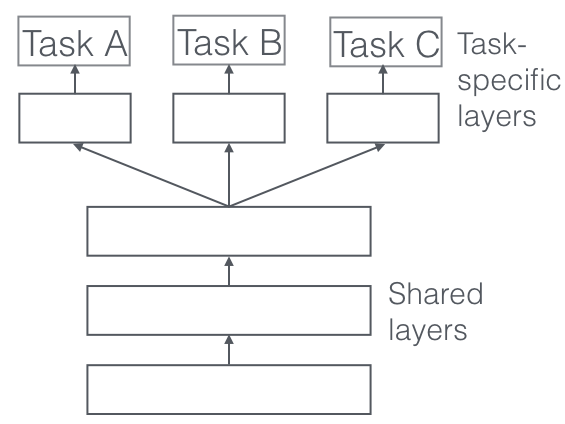
Advantage: reduce the risk of overfitting.
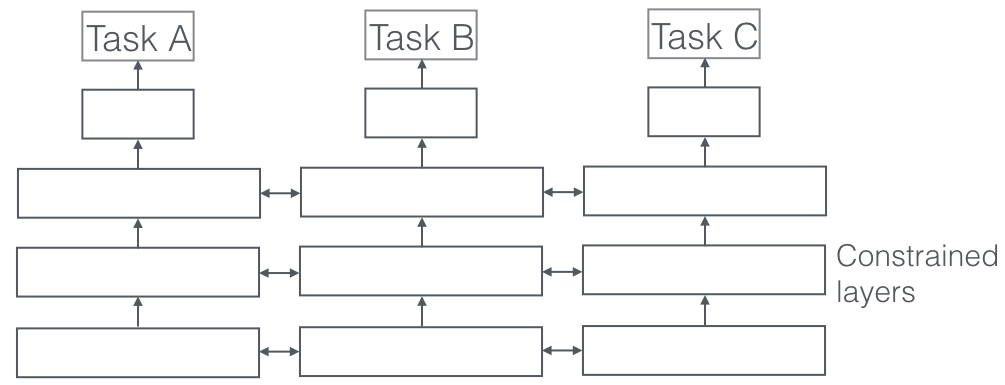
soft parameter sharing
each task has its own model with its own parameters. The distance between the parameter is regularized in order to encourage the parameter to be similar.
implicit data augmentation
Attention focusing
Eavesdropping
Representation bias
Regularization
Block-sparse regularization
We have T tasks, For each task t, we have a model $m_t$ with parameter $a_t$ of dimensionality d. We can write the parameters as a column vector $at=[a_{1,t} …a_{d,t}]^T$ We now stack a1,….,aT column by column to form a matrix A.(dxt). THe ith row contains the parameter ai corresponding to the i-th feature of the model for every task, while the j-th column of A contains the parameters $a_{.,j}$ corresponding to the j-th model.
### apply l1 norm: while in the single-task setting, the l1 norm is computed based on the parameter vector $a_t$ of the respective tasks t, for MTL we compute it over our task parameter matrix A. We first compute an $l_q$ norm across each row $a_i$ which yields a vector $b=[|a_1|_q,…,|a_d|_q]$. THen we compute the l1 norm of this vector, which forces all but a few entries of b to be 0.
As we can see, depending on what constraint we would like to place on each row, we can use a different $l_q$. In general, we refer to these mixed-norm constraints as $l_1/l_q$ norms. they are also known as block-sparse regularization
As much as this block-sparse regularization is intuitively plausible, it is very dependent on the extent to which the features are shared across tasks. [16] show that if features do not overlap by much, $ℓ_1/ℓ_q$ regularization might actually be worse than element-wise $ℓ_1$ regularization.
## Learning task relationships
### negative transfer
-
A global penalty which measures how large our column parameter vectors are on average: $\Omega_{mean}(A) = \bar{a} ^2$ - A measure of between-cluster variance that measures how close to each other the clusters are: $\Omega_{between}(A) = \sum^C_{c=1} T_c | \bar{a}_c - \bar{a} |^2$ where Tc is the number of tasks in the c-th cluster and $\bar{a}_c$ is the mean vector of the task parameter vectors in the c-th cluster.
- A measure of within-cluster variance that gauges how compact each cluster is : $\Omega_{within} = \sum^C_{c=1} \sum_{t \in J(c)} | a_{\cdot, t} - \bar{a}_c |^2$ where J(c) is the set of tasks in the c-th cluster.
final constraint:
$\Omega(A) = \lambda_1 \Omega_{mean}(A) + \lambda_2 \Omega_{between}(A) + \lambda_3 \Omega_{within}(A)$
## Recent work on MTL for Deep Learning
Deep Relation Networks
In MTL for computer vision, approaches often share the convolutional layers, while learning task-specific fully-connected layers
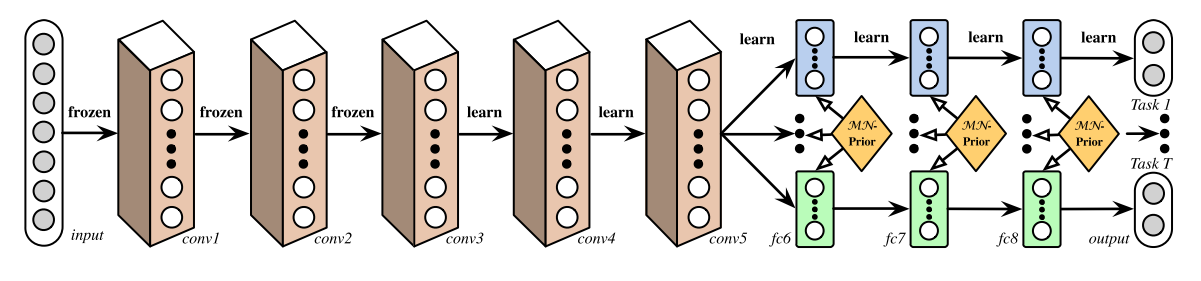
deep relation networks: they place matrix priors on the fully connected layers, which allow the model to learn the relationship between tasks.
Fully-Adaptive Feature Sharing
Starting at the other extreme, [39] propose a bottom-up approach that starts with a thin network and dynamically widens it greedily during training using a criterion that promotes grouping of similar tasks.
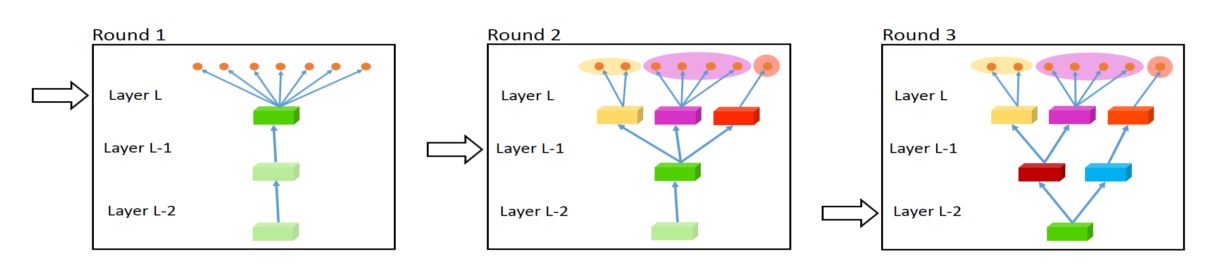figure 4: The widening procedure for fully-adaptive feature sharing.
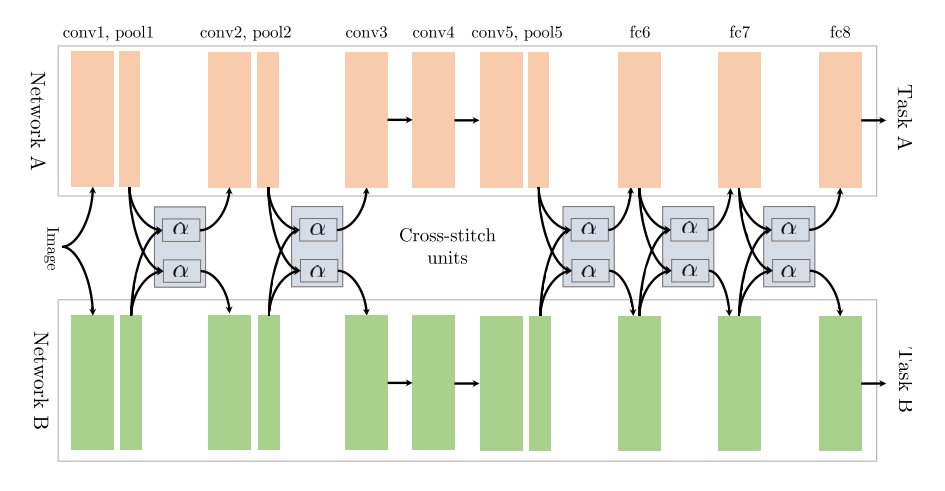
Cross-stitch Networks
start out with two separate model architectures just as in soft parameter sharing. They then use what they refer to as cross-stitch units to allow the model to determine in what way the task-specific networks leverage the knowledge of the other task by learning a linear combination of the output of the previous layers.
low-supervision
in NLP, recent work focused on finding better task hierarchies for multi-task learning.
hard parameter sharing quickly breaks down if tasks are not closely related or require reasoning on different levels. Recent approaches have thus looked towards learning what to share and generally outperform hard parameter sharing.
As mentioned initially, we are doing MTL as soon as we are optimizing more than one loss function.
